goglsick.blogg.se

The smallest altitude is then = or See Also 2002 AMC 10A ( Problems Now scale the triangle back up by multiplying every dimension by. The two altitudes and are known, and the area is therefore, and, which is clearly less than or. The triangle forms a right triangle, so we can first draw a triangle with legs and and hypotenuse. Since the side of length in the big triangle corresponds with our altitude, we take to get our answer or. The ratio of sides between that triangle and the bigger one is. This occurs because you end up with similar triangles which have proportional sides and the altitude is the long leg of 1 triangle and the short leg of the other similar triangle. There is a rule that states that the three triangles formed when the altitude is dropped (the big triangle and two smaller ones it gets split into) are similar! We take the triangle with hypotenuse. It turns out the when you drop an altitude (h in the picture below) from the the right angle of a right triangle, the length of the altitude becomes a geometric mean. All that is left is to check the altitude from the right angle vertex to the hypotenuse. The sides are in the ratio of, and are therefore a Pythagorean Triple and a part of a right triangle. īy Heron's formula, the area is, hence the shortest altitude's length is. Let the length be we have, so and is 12. To get the smallest altitude, it must be drawn to the hypotenuse. Since the area remains constant, the altitude and side to which it is drawn are inversely proportional. Now, consider an altitude drawn to any side. This is a Pythagorean triple (a actually) with legs and.

So the red line goes from (0,0) to (3.84, 2.88).Given a triangle with side lengths 15, 20, and 25, find the triangle's shortest altitude. 4/3x + 8 = 3/4x (multiply both sides by 12 to eliminate fractions) To find the point of intersection, we can set the two equations equal to each other: Since its y-intercept is 0, the equation of the red line is: Since the red line is perpendicular to the hypotenuse line, its gradient must be 3/4 (negative reciprocal or m*m = -1). Therefore the equation of the line of the hypotenuse is: Therefore the gradient (slope) is -8/6 = -4/3. The hypotenuse line goes through the points (6,0) and (0,8). The intersection between the extended base and the altitude is called the foot of the altitude. This line containing the opposite side is called the extended base of the altitude. forming a right angle with) a line containing the base (the opposite side of the triangle). So we can set up a proportion with the long legs and the hypotenuses. In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to (i.e. Substituting this new expression for the height, h, into the general formula for the area of a.

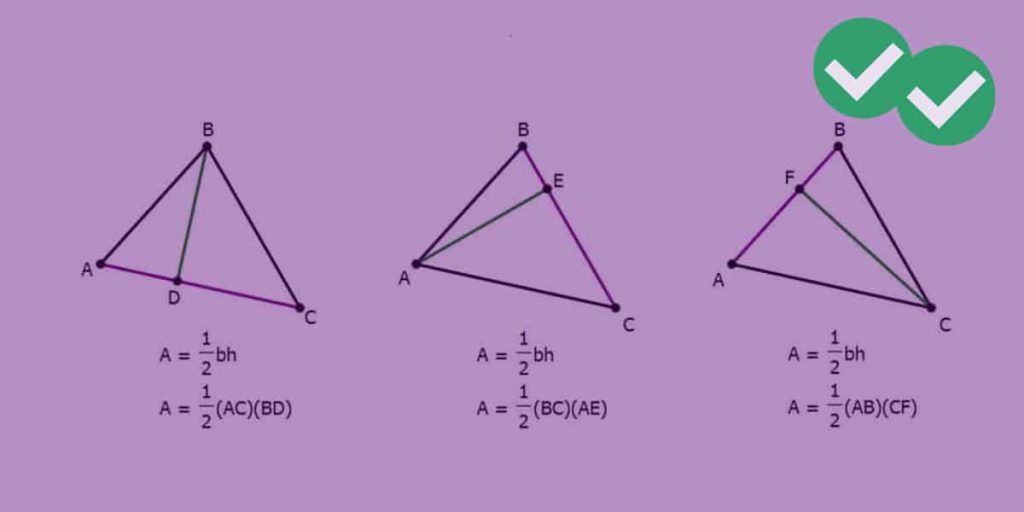
We know they are similar because they both have an angle of 90 degrees and they share the angle at the point (6,0). The height, h, of the triangle can be expressed as b sin C. I will work with the bottom triangle and the big triangle. The red line divides the big triangle into two smaller triangles, both of which are similar to the big triangle.

*note, you could also do this finding the top angle and using the upper triangle formed by the red line In this triangle 6 is the hypotenuse and the red line is the opposite side from the angle we found. We see that this angle is also in a smaller right triangle formed by the red line segment. We know that the legs of the right triangle are 6 and 8, so we can use inverse tan to find the base angle. Pythagoras tells us that the hypotenuse is 10 (6^2 + 8^2 = 10^2), and we already know the area of the triangle is 24, so 24 = 0.5(10)(red line) –> 24 = 5x –> x = 4.8. So it is also possible to calculate the area by doing 0.5(hypotenuse)(red line). But the red line segment is also the height of the triangle, since it is perpendicular to the hypotenuse, which can also act as a base. In a right triangle, we can use the legs to calculate this, so 0.5(8)(6) = 24. Here they are given based on the hint question: There are many methods to finding the answer. If we in the following triangle draw the altitude from the vertex of the right angle then the two triangles that are formed are similar to the triangle we.